Gamma process
This article may be too technical for most readers to understand. (October 2021) |
This article needs additional citations for verification. (June 2023) |
Also known as the (Moran-)Gamma Process,[1] the gamma process is a random process studied in mathematics, statistics, probability theory, and stochastics. The gamma process is a stochastic or random process consisting of independently distributed gamma distributions where represents the number of event occurrences from time 0 to time . The gamma distribution has shape parameter and rate parameter , often written as .[1] Both and must be greater than 0. The gamma process is often written as where represents the time from 0. The process is a pure-jump increasing Lévy process with intensity measure for all positive . Thus jumps whose size lies in the interval occur as a Poisson process with intensity The parameter controls the rate of jump arrivals and the scaling parameter inversely controls the jump size. It is assumed that the process starts from a value 0 at t = 0 meaning .
The gamma process is sometimes also parameterised in terms of the mean () and variance () of the increase per unit time, which is equivalent to and .
Plain English definition
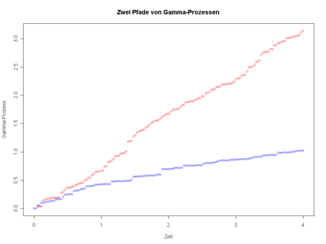
[edit]The gamma process is a process which measures the number of occurrences of independent gamma-distributed variables over a span of time. This image below displays two different gamma processes on from time 0 until time 4. The red process has more occurrences in the timeframe compared to the blue process because its shape parameter is larger than the blue shape parameter.
Properties
[edit]We use the Gamma function in these properties, so the reader should distinguish between (the Gamma function) and (the Gamma process). We will sometimes abbreviate the process as .
Some basic properties of the gamma process are:[citation needed]
Marginal distribution
[edit]The marginal distribution of a gamma process at time is a gamma distribution with mean and variance
That is, the probability distribution of the random variable is given by the density
Scaling
[edit]Multiplication of a gamma process by a scalar constant is again a gamma process with different mean increase rate.
Adding independent processes
[edit]The sum of two independent gamma processes is again a gamma process.
Moments
[edit]- The moment function helps mathematicians find expected values, variances, skewness, and kurtosis.
- where is the Gamma function.
Moment generating function
[edit]- The moment generating function is the expected value of where X is the random variable.
Correlation
[edit]Correlation displays the statistical relationship between any two gamma processes.
- , for any gamma process
The gamma process is used as the distribution for random time change in the variance gamma process.
Literature
[edit]- Lévy Processes and Stochastic Calculus by David Applebaum, CUP 2004, ISBN 0-521-83263-2.
References
[edit]- ^ a b Klenke, Achim, ed. (2008), "The Poisson Point Process", Probability Theory: A Comprehensive Course, London: Springer, pp. 525–542, doi:10.1007/978-1-84800-048-3_24, ISBN 978-1-84800-048-3, retrieved 2023-04-04