Converse nonimplication

Venn diagram of $P\nleftarrow Q$
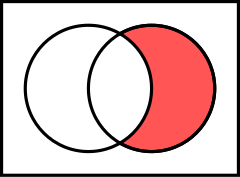
(the red area is true)

In logic, converse nonimplication^[1] is a logical connective which is the negation of converse implication (equivalently, the negation of the converse of implication).

Definition

Converse nonimplication is notated $P\nleftarrow Q$ , or $P\not \subset Q$ , and is logically equivalent to $\neg (P\leftarrow Q)$ and $\neg P\wedge Q$ .

Truth table

The truth table of $A\nleftarrow B$ .^[2]

$A$	$B$	$A\nleftarrow B$
F	F	F
F	T	T
T	F	F
T	T	F

Notation

Converse nonimplication is notated ${\textstyle p\nleftarrow q}$ , which is the left arrow from converse implication ( ${\textstyle \leftarrow }$ ), negated with a stroke ( $/$ ).

Alternatives include

${\textstyle p\not \subset q}$ , which combines converse implication's $\subset$ , negated with a stroke ( $/$ ).
${\textstyle p{\tilde {\leftarrow }}q}$ , which combines converse implication's left arrow ( ${\textstyle \leftarrow }$ ) with negation's tilde ( ${\textstyle \sim }$ ).
Mpq, in Bocheński notation

Properties

falsehood-preserving: The interpretation under which all variables are assigned a truth value of 'false' produces a truth value of 'false' as a result of converse nonimplication

Natural language

Grammatical

Example,

If it rains (P) then I get wet (Q), just because I am wet (Q) does not mean it is raining, in reality I went to a pool party with the co-ed staff, in my clothes (~P) and that is why I am facilitating this lecture in this state (Q).

Rhetorical

Q does not imply P.

Colloquial

Boolean algebra

Converse Nonimplication in a general Boolean algebra is defined as ${\textstyle q\nleftarrow p=q'p}$ .

Example of a 2-element Boolean algebra: the 2 elements {0,1} with 0 as zero and 1 as unity element, operators ${\textstyle \sim }$ as complement operator, ${\textstyle \vee }$ as join operator and ${\textstyle \wedge }$ as meet operator, build the Boolean algebra of propositional logic.

${\textstyle {}\sim x}$	$1$	$0$
$x$	$0$	$1$

and

$y$
$1$	$1$	$1$
$0$	$0$	$1$
${\textstyle y_{\vee }x}$	$0$	$1$	$x$

and

$y$
$1$	$0$	$1$
$0$	$0$	$0$
${\textstyle y_{\wedge }x}$	$0$	$1$	$x$

then

\scriptstyle {y\nleftarrow x}\!

means

$y$
$1$	$0$	$0$
$0$	$0$	$1$
$\scriptstyle {y\nleftarrow x}\!$	$0$	$1$	$x$

(Negation)

(Inclusive or)

(And)

(Converse nonimplication)

Example of a 4-element Boolean algebra: the 4 divisors {1,2,3,6} of 6 with 1 as zero and 6 as unity element, operators $\scriptstyle {^{c}}\!$ (co-divisor of 6) as complement operator, $\scriptstyle {_{\vee }}\!$ (least common multiple) as join operator and $\scriptstyle {_{\wedge }}\!$ (greatest common divisor) as meet operator, build a Boolean algebra.

$\scriptstyle {x^{c}}\!$	$6$	$3$	$2$	$1$
$x$	$1$	$2$	$3$	$6$

and

$y$
$6$	$6$	$6$	$6$	$6$
$3$	$3$	$6$	$3$	$6$
$2$	$2$	$2$	$6$	$6$
$1$	$1$	$2$	$3$	$6$
$\scriptstyle {y_{\vee }x}\!$	$1$	$2$	$3$	$6$	$x$

and

$y$
$6$	$1$	$2$	$3$	$6$
$3$	$1$	$1$	$3$	$3$
$2$	$1$	$2$	$1$	$2$
$1$	$1$	$1$	$1$	$1$
$\scriptstyle {y_{\wedge }x}$	$1$	$2$	$3$	$6$	$x$

then

\scriptstyle {y\nleftarrow x}\!

means

$y$
$6$	$1$	$1$	$1$	$1$
$3$	$1$	$2$	$1$	$2$
$2$	$1$	$1$	$3$	$3$
$1$	$1$	$2$	$3$	$6$
$\scriptstyle {y\nleftarrow x}\!$	$1$	$2$	$3$	$6$	$x$

(Co-divisor 6)

(Least common multiple)

(Greatest common divisor)

(x's greatest divisor coprime with y)

Properties

Non-associative

$r\nleftarrow (q\nleftarrow p)=(r\nleftarrow q)\nleftarrow p$ if and only if $rp=0$ #s5 (In a two-element Boolean algebra the latter condition is reduced to $r=0$ or $p=0$ ). Hence in a nontrivial Boolean algebra Converse Nonimplication is nonassociative. ${\begin{aligned}(r\nleftarrow q)\nleftarrow p&=r'q\nleftarrow p&{\text{(by definition)}}\\&=(r'q)'p&{\text{(by definition)}}\\&=(r+q')p&{\text{(De Morgan's laws)}}\\&=(r+r'q')p&{\text{(Absorption law)}}\\&=rp+r'q'p\\&=rp+r'(q\nleftarrow p)&{\text{(by definition)}}\\&=rp+r\nleftarrow (q\nleftarrow p)&{\text{(by definition)}}\\\end{aligned}}$

Clearly, it is associative if and only if $rp=0$ .

Non-commutative

$q\nleftarrow p=p\nleftarrow q$ if and only if $q=p$ #s6. Hence Converse Nonimplication is noncommutative.

Neutral and absorbing elements

$0$ is a left neutral element ( $0\nleftarrow p=p$ ) and a right absorbing element ( ${p\nleftarrow 0=0}$ ).
$1\nleftarrow p=0$ , $p\nleftarrow 1=p'$ , and $p\nleftarrow p=0$ .
Implication $q\rightarrow p$ is the dual of converse nonimplication $q\nleftarrow p$ #s7.

Converse Nonimplication is noncommutative
Step	Make use of	Resulting in
s.1	Definition	$\scriptstyle {q{\tilde {\leftarrow }}p=q'p\,}\!$
s.2	Definition	$\scriptstyle {p{\tilde {\leftarrow }}q=p'q\,}\!$
s.3	s.1 s.2	$\scriptstyle {q{\tilde {\leftarrow }}p=p{\tilde {\leftarrow }}q\ \Leftrightarrow \ q'p=qp'\,}\!$
s.4		$\scriptstyle {q\,}\!$	$\scriptstyle {=\,}\!$	$\scriptstyle {q.1\,}\!$
s.5	s.4.right - expand Unit element		$\scriptstyle {=\,}\!$	$\scriptstyle {q.(p+p')\,}\!$
s.6	s.5.right - evaluate expression		$\scriptstyle {=\,}\!$	$\scriptstyle {qp+qp'\,}\!$
s.7	s.4.left = s.6.right	$\scriptstyle {q=qp+qp'\,}\!$
s.8		$\scriptstyle {q'p=qp'\,}\!$	$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {qp+qp'=qp+q'p\,}\!$
s.9	s.8 - regroup common factors		$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {q.(p+p')=(q+q').p\,}\!$
s.10	s.9 - join of complements equals unity		$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {q.1=1.p\,}\!$
s.11	s.10.right - evaluate expression		$\scriptstyle {\Rightarrow \,}\!$	$\scriptstyle {q=p\,}\!$
s.12	s.8 s.11	$\scriptstyle {q'p=qp'\ \Rightarrow \ q=p\,}\!$
s.13		$\scriptstyle {q=p\ \Rightarrow \ q'p=qp'\,}\!$
s.14	s.12 s.13	$\scriptstyle {q=p\ \Leftrightarrow \ q'p=qp'\,}\!$
s.15	s.3 s.14	$\scriptstyle {q{\tilde {\leftarrow }}p=p{\tilde {\leftarrow }}q\ \Leftrightarrow \ q=p\,}\!$

Implication is the dual of Converse Nonimplication
Step	Make use of	Resulting in
s.1	Definition	$\scriptstyle {\operatorname {dual} (q{\tilde {\leftarrow }}p)\,}\!$	$\scriptstyle {=\,}\!$	$\scriptstyle {\operatorname {dual} (q'p)\,}\!$
s.2	s.1.right - .'s dual is +		$\scriptstyle {=\,}\!$	$\scriptstyle {q'+p\,}\!$
s.3	s.2.right - Involution complement		$\scriptstyle {=\,}\!$	$\scriptstyle {(q'+p)''\,}\!$
s.4	s.3.right - De Morgan's laws applied once		$\scriptstyle {=\,}\!$	$\scriptstyle {(qp')'\,}\!$
s.5	s.4.right - Commutative law		$\scriptstyle {=\,}\!$	$\scriptstyle {(p'q)'\,}\!$
s.6	s.5.right		$\scriptstyle {=\,}\!$	$\scriptstyle {(p{\tilde {\leftarrow }}q)'\,}\!$
s.7	s.6.right		$\scriptstyle {=\,}\!$	$\scriptstyle {p\leftarrow q\,}\!$
s.8	s.7.right		$\scriptstyle {=\,}\!$	$\scriptstyle {q\rightarrow p\,}\!$
s.9	s.1.left = s.8.right	$\scriptstyle {\operatorname {dual} (q{\tilde {\leftarrow }}p)=q\rightarrow p\,}\!$

Computer science

An example for converse nonimplication in computer science can be found when performing a right outer join on a set of tables from a database, if records not matching the join-condition from the "left" table are being excluded.^[3]

References

^ Lehtonen, Eero, and Poikonen, J.H.
^ Knuth 2011, p. 49
^ "A Visual Explanation of SQL Joins". 11 October 2007. Archived from the original on 15 February 2014. Retrieved 24 March 2013.

Knuth, Donald E. (2011). The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1 (1st ed.). Addison-Wesley Professional. ISBN 978-0-201-03804-0.

External links

Media related to Converse nonimplication at Wikimedia Commons

[1] Lehtonen, Eero, and Poikonen, J.H.

[Knuth-2] Knuth 2011, p. 49

[3] "A Visual Explanation of SQL Joins". 11 October 2007. Archived from the original on 15 February 2014. Retrieved 24 March 2013.

[1]

[2]

[3]

v t e Common logical connectives
Tautology/True $\top$
Alternative denial (NAND gate) $\uparrow$ Converse implication $\leftarrow$ Implication (IMPLY gate) $\rightarrow$ Disjunction (OR gate) $\lor$
Negation (NOT gate) $\neg$ Exclusive or (XOR gate) $\not \leftrightarrow$ Biconditional (XNOR gate) $\leftrightarrow$ Statement (Digital buffer)
Joint denial (NOR gate) $\downarrow$ Nonimplication (NIMPLY gate) $\nrightarrow$ Converse nonimplication $\nleftarrow$ Conjunction (AND gate) $\land$
Contradiction/False $\bot$
Philosophy portal

Definition

Truth table

Notation

Properties

Natural language

Grammatical

Rhetorical

Colloquial

Boolean algebra

Properties

Non-associative

Non-commutative

Neutral and absorbing elements

Computer science

References

External links

Pfad - The Proxy pFad of © 2024 Garber Painting. All rights reserved.