Conjunción lógica

En razonamiento formal, una conjunción lógica ( $\land$ ) entre dos proposiciones es un conector lógico cuyo valor de la verdad resulta en cierto solo si ambas proposiciones son ciertas, y en falso de cualquier otra forma.​ Existen diferentes contextos donde se utiliza la conjunción lógica.

Conjunción lógica
Diagrama de Venn de la conectiva
Nomenclatura
Lenguaje natural	A y B A pero B
Lenguaje formal	$A\land B$
Operador booleano	$\land$
Operador de conjuntos	$\cap$
Puerta lógica
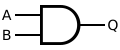Tabla de verdad
${\begin{array}{c|c||c}A&B&A\land B\\\hline V&V&V\\V&F&F\\F&V&F\\F&F&F\\\end{array}}$

En lenguajes formales, el conectivo "y" se utiliza en español para simbolizar una conjunción lógica. La noción equivalente en la teoría de conjuntos es la intersección ( $\cap$ ). En álgebra booleana, la conjunción como operador binario entre dos variables se representa con el símbolo de punto medio ( · ).

En electrónica, una puerta AND es una puerta lógica que implementa la conjunción lógica.

Lógica de proposiciones

Siendo ${\mathcal {P}}$ el conjunto de proposiciones, y $a,b,c,d,\dots$ proposiciones de ${\mathcal {P}}$, se puede definir la operación binaria: conjunción, por la que a una variable $c\,$ de ${\mathcal {P}}$ se le asigna el valor de la conjunción del par ordenado de la variables $(a,b)$ de ${\mathcal {P}}\times {\mathcal {P}}$.

${\begin{array}{rccl}\land :&{\mathcal {P}}\times {\mathcal {P}}&\longrightarrow &{\mathcal {P}}\\&(a,b)&\mapsto &c=\land (a,b)\;\equiv \;c=a\land b\end{array}}$

Definición

Dado un conjunto universal U formado por los elementos falso: F y verdadero: V:

$U=\{F,V\}$

y una operación binaria interna conjunción $\land$, que representaremos $(U,\land )$:

${\begin{array}{rccl}\land :&\;U\times U&\to &U\\&(a,b)&\to &c=a\land b\end{array}}$

por la que definimos una aplicación que a cada par ordenado (a,b) de U por U se le asigna un c de U.

$\forall (a,b)\in U\times U\,:\quad \exists !c\in U\;/\quad c=a\land b$

Para todo par ordenado (a,b) en U por U, se cumple que existe un único c en U, tal que c es el resultado de la conjunción lógica a y b.

Usos

Lenguaje formal

Si declaraciones en un lenguaje formal representan proposiciones en lógica proposicional con contenido de verdad o falsedad, entonces una conjunción lógica es cierta solo si ambas declaraciones son ciertas.

Álgebra Booleana

Dado un conjunto B = {0, 1}, se define · como una función tal que:

0 · 0 = 0, 0 · 1 = 0, 1 · 0 = 0, 1 · 1 = 1

Propiedades

La conjunción lógica presenta las siguientes propiedades:

• 1. La ley asociativa:

$\forall a,b,c\in U:\;(a\land b)\land c=a\land (b\land c)$

• 2. Existencia del elemento neutro:

$\forall a\in U:\;a\land V=a$

• 3. La ley conmutativa:

$\forall a,b\in U:\;a\land b=b\land a$

• 4. Ley distributiva de la conjunción respecto de la disyunción:

$\forall a,b,c\in U:\;a\land (b\lor c)=(a\land b)\lor (a\land c)$

• 5. Existe elemento complementario:

$\forall a\in U;\;\exists \lnot {a}\in U:\;a\land \lnot {a}=F$

• 6. Conjunción versus disyunción

$\forall a,b\in U:\;a\land b\rightarrow a\lor b$

Operación con bits

La conjunción es utilizada a menudo para operaciones con bits. Por ejemplo:

• Cero y cero:

$0\land 0=0\quad \longleftrightarrow \quad {\begin{array}{cc}&0\\\land &0\\\hline &0\\\end{array}}$

• Cero y uno:

$0\land 1=0\quad \longleftrightarrow \quad {\begin{array}{cc}&0\\\land &1\\\hline &0\\\end{array}}$

• Uno y cero:

$1\land 0=0\quad \longleftrightarrow \quad {\begin{array}{cc}&1\\\land &0\\\hline &0\\\end{array}}$

• Uno y uno:

$1\land 1=1\quad \longleftrightarrow \quad {\begin{array}{cc}&1\\\land &1\\\hline &1\\\end{array}}$

• Para cuatro bit:

$1010\land 1100=1000\quad \longleftrightarrow \quad {\begin{array}{ccccc}&1&0&1&0\\\land &1&1&0&0\\\hline &1&0&0&0\\\end{array}}$

Véase también

• Álgebra booleana
• Lógica proposicional
• puerta lógica
• Disyunción lógica
• Operador a nivel de bits

Bibliografía

• Nachbin, Leopoldo (1986). Álgebra elemental. Rochester, Nueva York: Eva V. Chesnau. Edición de la OEA, traducida al español por César E. Silva.
• Libros relacionados en formato PDF

Enlaces externos

• Lógica de enunciados

• Datos: Q191081
• Multimedia: Logical conjunction / Q191081